Online Classes, Assignment and Mentoring

What you will learn in this section

• Finding Cosne function formula for sum and addition of angles
• Finding Sine function formula for sum and addition of angles
• Finding Tangent function formula for sum and addition of angles
• Finding exact value of Sine, Cosine and Tangent value using these formula

What we assume you have already learnt

• Meaning and formulae of trigonometric expressions
• cos²A + sin²A = 1
• Cos(-A) = CosA and Sin(-A) = -SinA

Sum and difference of angles

If A and B are two angles,

• Sum of angles= A + B
• Difference of angle = A – B
• Multiple angles = nA where n is an integer. e.g. 2, 3A etc

When we say sum and difference of angles, we mean

Cosine of sum and difference of angles

Let us say we have a unit circle centered at O. We will take horizontal radius as base of our calculation. The point P(1,0) is the point where our reference/base meets the circumference.

Let A and B be points on circumference such that  ∠ AOP = α and ∠ BOA = β;

This also means:
∠BOP = (α + β)

Let us draw an angle -β on OP such that it meets the circumference at B’. ∠ POB’ = -β

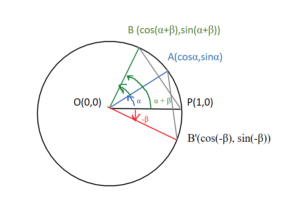
Coordinates of all points in the diagram:

• O(0,0)
• P(1,0)
• A (cosα, sinα)
• B (cos(α + β), sin(α + β))
• B'(cos(-β), sin(-β))

The distance between B and P is same as the distance between A and B’. i.e.

√(cos(α + β)-1)² + (sin(α + β) – 0)² = √(cosα-cos(-β))² + (sinα – sin(-β))²
squaring both the sides:
(cos(α + β)-1)² + (sin(α + β) – 0)² = (cosα-cos(-β))² + (sinα – sin(-β))²
or
cos²(α + β) -2cos(α + β) +1 + sin²(α + β) = (cosα-cos(β))² + (sinα + sin(β))²
{since cos(-β) = cosβ and sin(-β) = -sinβ);
or
2 – 2cos(α + β) = cos²α – 2cosαcosβ + cos²β+ sin²α + 2sinαsinβ + sin²β
or
2 – 2cos(α + β) = <U>cos²α + sin²α </U>+ ??<U>cos²β + sin²β </U>+ 2sinαsinβ – 2cosαcosβ
or
2 – 2cos(α + β) = 2 + 2sinAsinB – 2cosαcosβ
or
-2cos(α + β) = 2sinAsinB – 2cosαcosβ
or
cos(α + β) = 2cosαcosβ – 2sinAsinB

this can be rewritten as: 

cos(A + B) = cosAcosB – sinAsinB

In the above formula, if we replace B by -B, we will have:

cos(A + (- B)) = cosAcos(-B) – sinAsin(-B)
or
cos(A – B) = cosAcosB + sinAsinB [since cos(-B) = cos B and sin(-B) = -sinB

Usage

Find the value of cos75^o

We can write cos75^o as
cos(45 + 30)^o = cos45^ocos30^o – sin45^osin30^o
= (1/√2)*(√3/2) – (1/√2)*(1/2)
= (√3-1)/2√2

or

Sine of sum and difference of angles

In the figure given below, Let us say ∠ABC = α and ∠PBA = β ∠PBC = α+β Also, BP = CA AP is parallel to BC

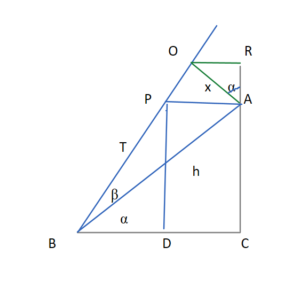
Let us extend BP and CA. Draw a perpendicular on AB at A such that it meets BP at O. Also draw OR parallel to BC. So, ∠OAR = α

Let’s say AB = h, OB = T and OA = x

then sinβ = x/T or x = T*sinβ and h = T*cosβ
AC = hsinα = T*sinα*cosβ —– (i)
AR = xcosα = T*cosα*sinβ —– (ii)

sin(α+β) = RC/T or
sin(α+β) = (AR + AC)/T —– (iii)

substituting values of AR and AC from (i) and (ii) into (iii), we get

sin(α+β) = (T*sinα*cosβ + T*cosα*sinβ)/T
dividing numerator and denominator by T, we get

For multiple and submultiple angles, please click here.