Logarithm and Exponentials
Logarithm and Exponentials are two of the important tools used in Mathematics. Here are some quick tips on the two functions
Exponentials
- Multiplication is repeated addition
- Repeated multiplication is represented by exponents.
- Here are the properties of exponents.
- For laws governing exponential operations, please refer to this page.
- am*an = a(m+n)
- (abcd)n = an * bn * cn * dn
- (a⁄b)n = an⁄bn
- (-a)n = (-1)n * an = -an if n is odd andan if n is even
- (am)n = amn
- a-n = 1⁄an
- (a⁄b)-n = (b⁄a)n
- am⁄ an = am-n if m> n = 1⁄a(n-m) if n> m
- a0 = 1
= 1 if m = n
Logarithm
Division and multiplication are complicated mathematical operations as compared to addition and subtraction, especially when digits are large or fractions or decimals are involved.
When navigation increased, the need for a simpler method arose. This where logarithm came into play.
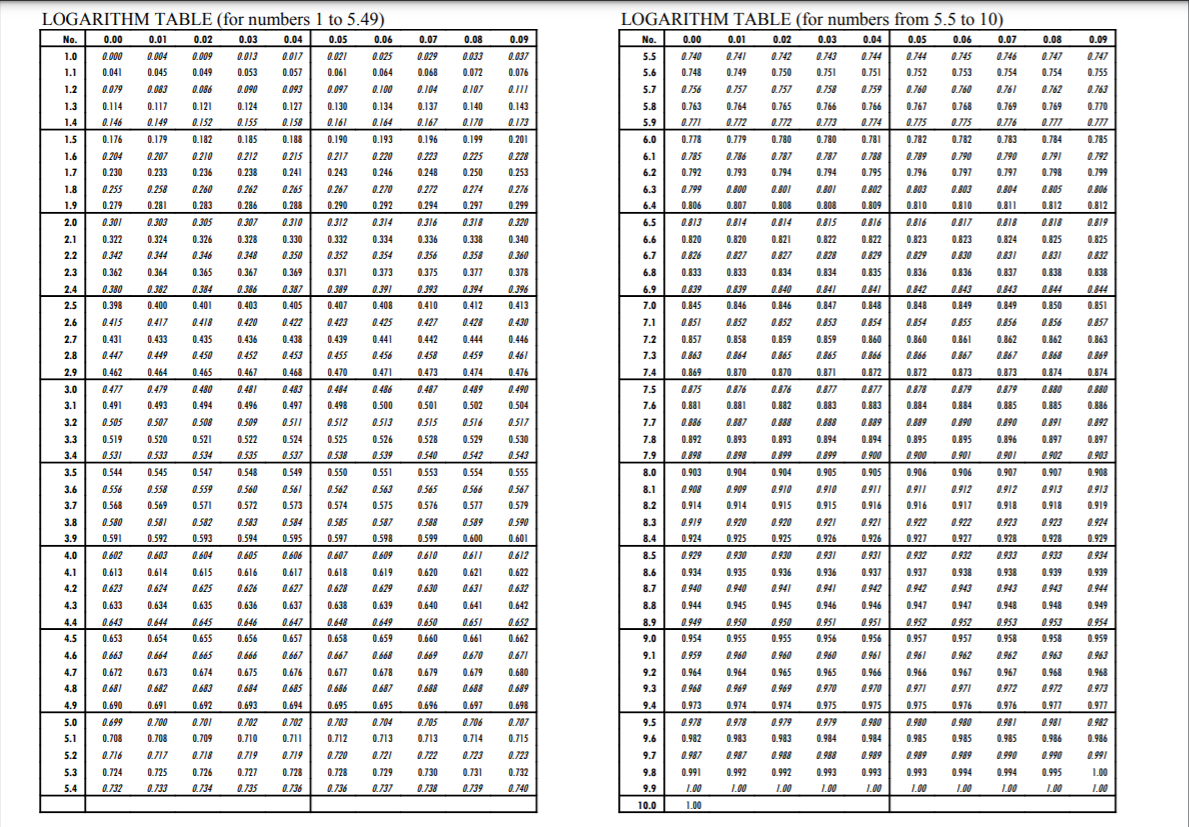
Log expressions are written in the form: LogaN where a is the base.
Common logarithm has a base of 10 whereas e is used as a base for mathematical calculation. Log
Basic properties
As you can see on the right hand side, log helps transform multiplication and division into addition and subtraction.
e.g. if P = 2 x 3.
log P = log 2 + log 3
from the table below
log P = 0.301 + 0.477 = 0.778 = log 6,
which gives us
P = 6
log P = log 2 + log 3
from the table below
log P = 0.301 + 0.477 = 0.778 = log 6,
which gives us
P = 6
of logarithm function
- If ax = N then LogaN = x
- alogaN = N
- loga(pq) = loga(p) + loga(q)
- loga(p/q) = loga(p) – loga(q)
- loga(pm) =mlogap
- loga(p1/m) =(1/m)logap
- ln N = (log N)/(log e)
Logarithm Table