Geometric shapes, Perimeter, Area, Surface Area, Volume are some of the words that we come across frequently while studying geometry.
Below you will find some quick grabs on this topic
Key Terminologies related to shapes, perimeter and area
Poly = ‘Many’ Gon = ‘Angle’
A geometric shape formed by multiple angles or sides is called a polygon. example: Traingle, Rectangle etc.
Poly = “Many’ Hedron = ‘Face’
A 3 dimensional geometric shape with multiple faces, edges and vertices, in such a way that each vertex connects multiple faces joining, is called a polyhedron. ex: Cube, Cuboid etc
A flat surface which makes boundary of a polyhydron is called the face of the polyhydron.
A vertex is a corner point of a polygon or a polyhedron formed by the intersection of their edges or faces.
A vertex is a corner point of a polygon or a polyhedron formed by the intersection of their edges or faces.
Plural of vertex is vertices.
A segment that joins the polygon’s center to the midpoint of any side that is perpendicular to that side.
To find the apothem, In a regular polygon, divide the length of one side by 2 times the tangent of 180 degrees divided by the number of sides.
In a 2 dimensional figure, the surface occupied by the polygon is called its area.
To calculate area of a regular polygon:
A = 0.5 x perimeter x length of Apothem
The surface area of a polyhedron is the sum of the area of all of its faces.
S.A = Σ (area of all faces of the polygon)
Said another way, the surface area is the total area covered by the net of a polyhedron
Volume is the space enclosed by the boundary occupied by the 3-dimensional shape
Formulae
l = length b = breadth d = diagonal r = radius h = height
| Shape | Diagram | Properties | Perimeter | Area |
|---|---|---|---|---|
| Rectangle | 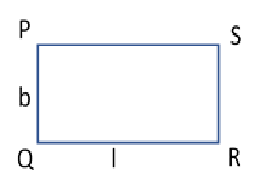 |
| 2* (l+b) | l*b |
| Square | 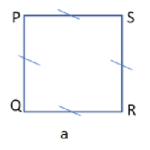 | All properties of a rectangle +
| 4*l | l2 |
| Parallelogram | 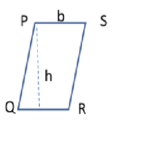 |
| 2*(l1+l2) | b*h |
| Rhombus | 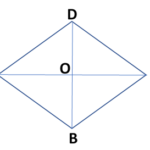 | All properties of a parallelogram +
| 4*l | d1*d2 |
| Trapezium | 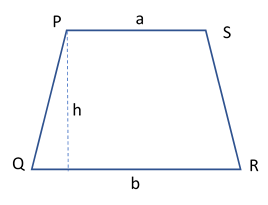 | • One set of sides are parallel | ½ * (l1+l2)*h | |
| Kite | 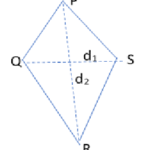 | 2 sets of adjacent sides are equal Diagonals bisect each other at right angle | 2*(l1+l2) | d1*d2 |
| Circle | 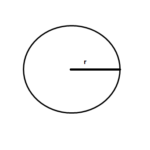 | All points on circumference is equidistant from a point called center The distance from center ti the circumference is called radius | 2πr | πr2 |
| Right Angle Triangle | 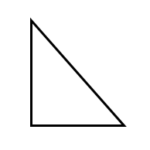 | Follows Pythogorus theorem h2 = l2 + b2 Sides are in pythogorous triad format | ½ * b*h | |
| Equilateral Triangle | 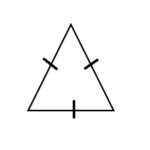 | all sides of the triangle are of equal length Angle bisectors meet the mid point of opposite side at 900 | 3*l | (√3l2)/4 |
| Shape | Shape | Properties | Surface Area | Volume |
|---|---|---|---|---|
| Cube | 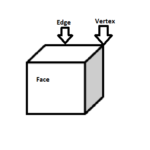 |
All faces and all edges are of the same dimension | 6l2 | l3 |
| Cuboid |  |
2*(l*b+B*h+l*h) | l*b*h | |
| Cylinder |  |
2πr(r+h) | π r2h | |
| Cone |  |
πr*(r+ √( h2+r2) | πr2h/3 |
To get complete details, including content, assignments and guidance, on chapters of Mensuration, please
